I'm getting better at scripting FreeCAD and I'm using to explore some very cool symmetries in the Platonic solids. Join me as we explore the cubes and platonic solids embedded in the geometry of an icosahedron.

To make an icosahedon, it turns out you don't need to calculate angles or lengths if you start with a Golden rectangle:

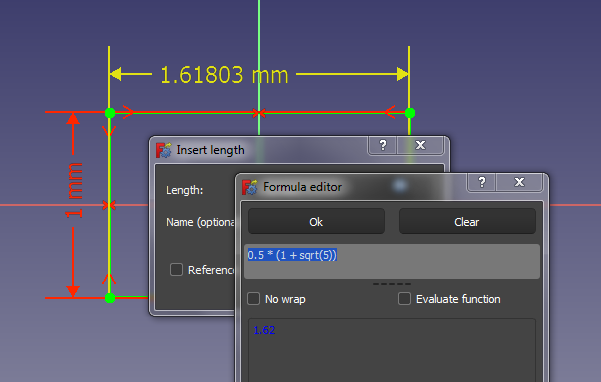
Make three golden rectangles, perpendicular to each other and not intersecting

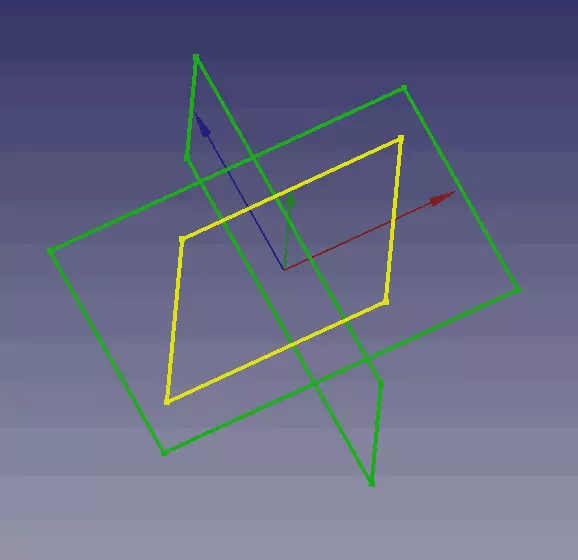
Connect the corners, and you get an icosahedron, the 20-sided Platonic solid where all sides and angles are equal:

Here's a solid view of the icosahedron with all the sides 5/

Now for the fun part! From the center of each face, draw a line to the center of every other face. That's a lot of lines! (I wrote a FreeCAD Python script to do this.)

There's a lot of symmetry going on! Outside is a dodecahedron, the dual of the icosahedron.

Here's the dodecahedron. Where a icosahedron has a vertex, the dodecahedron has a face, and vice-versa

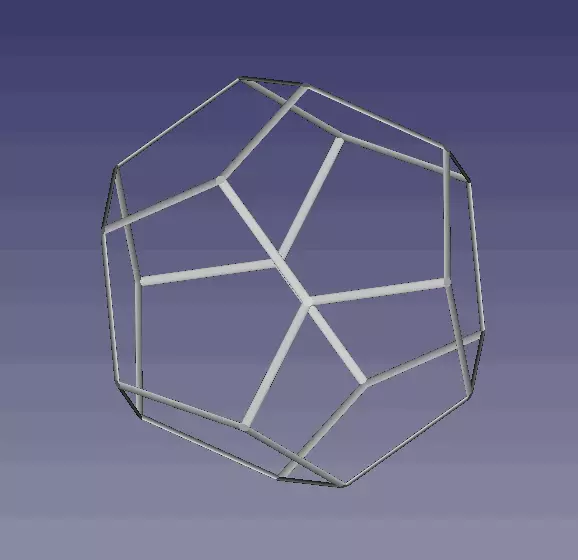
Let's subtract the dodecahedron. See anything else?

How about cubes?

Turns out there are 5 of them: Each dodecahedral side contains a pentagram, and each strut of the pentagram is the edge of a cube!

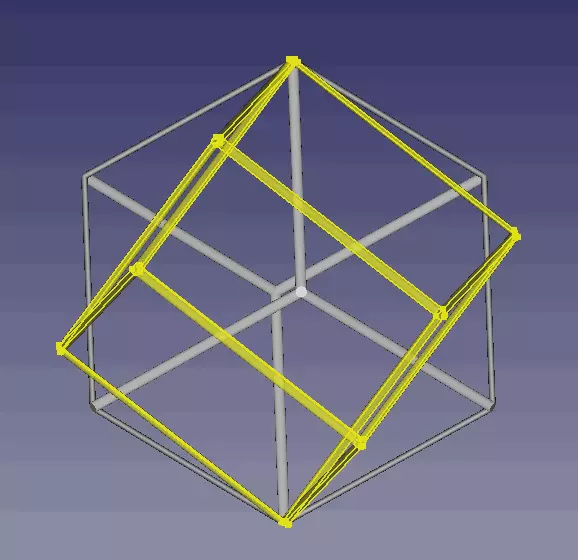
But there's more! If we hide the cubes, we can see... tetrahedrons!

There are ten tetrahedrons! Together they look like this. This is a "Compound of ten tetrahedra"" and it is its own dual.

If we hide the ten tetrahedrons, we are left with this:

In green above is the central starburst formed by lines between opposite faces. If we hide the central star, we're left with this. Can you spot the platonic solid here?

This is a great stellated dodecahedron, but inside is a baby icosahedron, like we started with! If you wanted to you coud draw lines between the face centers of that, and repeat this process recursively. Polyhedra all the way down!

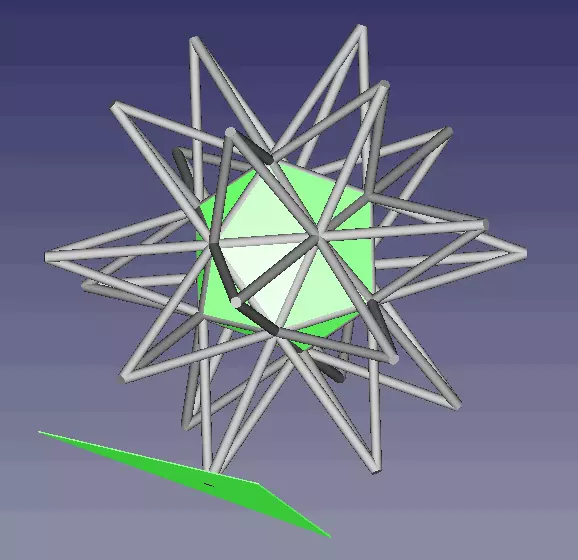
So here we've found 4 of the 5 Platonic solids: cubes, tetrahedra, dodecahedra, and icosahedra. I feel like there must be octohedra in there as well, can you find one? Or more??)